# Read the favicon image in binary mode
import os
def read_file(file_path):
with open(file_path, 'rb') as file: # Open the file in binary mode
return file.read()
file_path = os.getcwd() + '/favicon-16x16.png'
data = read_file(file_path)Knowing that computers use binary language, yet as a Python programmer, I haven’t had much chance to work with binary and hexadecimal in usual programming tasks. Binary numbers didn’t feel close to me. Since high-level programming like Python deals with abstract data types. Binary were looked rather theoretical.
However, when I came across a problem required to handle exponential values of 2, I found out practical side of binary and hexadecimal. This article provides a brief review of binary and hexadecimal representation in Python, along with their role in computer architecture and real-world applications.
Despite the fact that binary and hexadecimal systems are fundamental to computer science, many programmers don’t often directly handle these number systems in their day-to-day task. Nevertheless, understanding and utilizing these number system is crucial in various aspects of programming and computer science.
It’s important to note that binary can be used to represent anything in computing, from text and images to video and beyond. As we delve into this topic, we’ll explore how these number systems play a vital role in both low-level and high-level programming.
Unit of Data
Computer only understands binary language, which is a combination of 0s and 1s. It is the reason why binary and hexadecimal are basis of all data representation in computer. Although we are not familiar with these number systems, we are close to the terms of ‘Kilobyte(KB)’, ‘Megabyte(MB)’, ‘Gigabyte(GB)’ and ‘Terabyte(TB)’.
1 TB is equals to 1024 GB, 1 GB is equals to 1024 MB and it works same on others. In general, Kilo means 1000, Mega means 1,000,000, Giga means 1,000,000,000 and Tera means 1,000,000,000,000. those units are increased the power of 1000. However, when it comes to computer, it is not 1000, it is 1024. Why? Because every unit of data is represented in binary number. Considering this, we can easily found the reason why computer system use 1024 ($2^{10}), which is the nearest power of 2 to 1000.
It is hard to understand that every text, image, video and other data are represented in terms of 0s and 1s. But you can easily check it by opening any file in binary mode. Let’s see how it works.
Binary Representation with open() Function
My favicon image is 16x16 pixels and it is a PNG file like below. Let’s read the file in binary mode and see the first 5 bytes of it.
The variable data could be shown both in an image and in binary format.
First, you can see the favicon image below. The normal format of the image.
# Display the favicon image
from PIL import Image
from IPython.display import display
favicon_img = Image.open(file_path)
display(favicon_img)
Whereas, the binary format of the image is as follows:
# Display the first 5 bytes of the file in binary
for b in (data[:5]):
print(bin(b), end=" ")0b10001001 0b1010000 0b1001110 0b1000111 0b1101 Python has three type of main file objects: text file, buffered binary file and raw binary file. open() function is the canonical way to create a file object. It takes two arguments: file path and mode.
Files can be opened in two modes: text mode and binary mode. Text mode is for text data, binary mode is for non-text data like images, audio, etc. Binary mode does not perform any encoding or decoding. It reads and writes data as it is.
To open a file in binary mode, you need to add b to the mode string. For example, rb for reading and wb for writing. With this binary mode, you can get the bytes object instead of str object. A bytes object is a sequence of integers in the range of 0 to 255. This is why the output of the code below is range of 0 to 255, not 0 or 1.
# Open a file in binary mode
for b in (data[:5]):
print((b), end=" ")137 80 78 71 13 For more information, you can check the official Python documentation:
Basis unit of information: Bit and Byte
As you can see, my favicon image is represented in binary format. The first 5 bytes of the image are as follows:
0b10001001 0b1010000 0b1001110 0b1000111 0b1101In case of ‘0b10001001’, ‘0b’ is a prefix to indicate that the number is in binary format. The number itself is 10001001. Each digit in binary number is called a bit, which is the smallest unit of signal in a computer science. Bit is a short form of binary digit.
Bit only can have two values, 0 or 1 (off or on). \(N\) bits can represent \(2^{N}\) values. It is too small to indicate any meaningful data. Therefore, it is grouped into a larger unit called byte, which is the basic unit of data.
In the above example, 10001001 is consisted of 8 bits. As you can see, 1 byte can represent \(2^{8}\) or 256 values. Does byte enough to describe information? Yes, it is. For example, 1 byte is enough to indicate a character in ASCII code. This is why the byte is the basic unit of data in computer science. Since the basic unit of data is byte, every unit of data is ends with ‘byte’. For example, kilobyte, megabyte, gigabyte, terabyte, etc. are all ends with ‘byte’.
Hexadecimal: Compact Representation of Binary Data
What about hexadecimal? Hexadecimal is a numeric system that based on 16. It uses 16 symbols: 0-9 and A-F, the most compact way to compress binary data. For example, only 2 digits are enough to indicate number 255 in hexadecimal, whereas 8 digits are needed in binary, like 0b11111111. Namely, 1 byte can be represented by 2 hexadecimal digits.
Still computer uses binary number, hexadecimal is compromise between programmer and computer. It is easier to read and write than binary, also easily convert to binary. This is why hexadecimal is widely used in computer science, especially in low-level programming: expressing memory addresses, register values, and other byte based data, for instance.
Practical Use of Binary and Hexadecimal in Python
Convert between number systems
Convert different base numbers to decimal
Python provides built-in functions to convert different base numbers to decimal.
Binary numbers are string of 0s and 1s. To convert binary to decimal, int function can be used with base 2. Normally, int function takes one argument, which is a string of number. However, int function can takes two arguments: number and base. For example, int('1010', 2) converts binary number ‘1010’ to decimal number 10.
# Convert binary to decimal
# class int( x: str | bytes | bytearray, /, base: SupportsIndex) -> int
binary_num = '1010'
decimal_num = int(binary_num, 2)
print(f"Binary number {binary_num} is converted to decimal number {decimal_num}")Binary number 1010 is converted to decimal number 10Likewise, hexadecimal number can be converted to decimal number. Since hex numbers are described of 0-9 and A-F, its data type is string. To convert hexadecimal to decimal, int function can be used with base 16. For example, int('FF', 16) converts hexadecimal number ‘FF’ to decimal number 255.
# Convert hexadecimal to decimal
hex_num = 'FF'
decimal_num = int(hex_num, 16)
print(f"Hexadecimal number {hex_num} is converted to decimal number {decimal_num}")Hexadecimal number FF is converted to decimal number 255Convert decimal to different base numbers
To convert decimal number to binary or hexadecimal, bin and hex functions can be used. bin function converts decimal number to binary number. hex function converts decimal number to hexadecimal number.
# Convert decimal to binary
# (function) def bin(number: int | SupportsIndex, / ) -> str
decimal_num = 10
binary_num = bin(decimal_num)
print(f"Decimal number {decimal_num} is converted to binary number {binary_num}")Decimal number 10 is converted to binary number 0b1010# Convert decimal to hexadecimal
# (function) def hex(number: int | SupportsIndex, / ) -> str
decimal_num = 255
hex_num = hex(decimal_num)
print(f"Decimal number {decimal_num} is converted to hexadecimal number {hex_num}")Decimal number 255 is converted to hexadecimal number 0xffBitwise Operations
Bitwise operations are performed on binary numbers. These operators are particularly useful when dealing with binary representations directly. In certain situations, it significantly improves the performance of the code as well.
The main bitwise operators in Python are:
&(AND): Returns 1 if both bits are 1.|(OR): Returns 1 if either of the bits is 1.^(XOR): Returns 1 if the bits are different.~(NOT): Inverts the bits.<<(Left Shift): Shifts the bits to the left.>>(Right Shift): Shifts the bits to the right.
Difference between bitwise and logical operators
In Python, there are bitwise operators (&, |, ~) and their logical counterparts (and, or, not). While the basic concepts are similar, their implementations differ. Both & and and return True when both conditions are True, but & operates on individual bits. Similarly, | and or, as well as ~ and not, have analogous functions but work at different levels of abstraction. These operators may seem interchangeable, in some situations, yet understanding their differences is crucial.
# Bitwise AND operator
print(f"Bitwise AND: {5 & 8}")
print(f"Logical AND: {5 and 8}")Bitwise AND: 0
Logical AND: 8Why does the output differ? The & operator works on individual bits, whereas the and operator evaluates compare the entire expression of operands: 5, 8.
# Binary representation of 5 and 8
print(f"Binary of 5: {bin(5)}")
print(f"Binary of 8: {bin(8)}")Binary of 5: 0b101
Binary of 8: 0b1000The binary representation of 5 and 8 are 0b101 and 0b1000, respectively. The bitwise AND operation is performed on each bit of the two numbers. There are no common digits/numbers/bits between 5 and 8. Therefore the result is 0b0, which is 0 in decimal.
What about the logical AND operation? The and operator evaluates the truth of the entire expression. In this case, both 5 and 8 are considered True in Python. The and operator returns the second operand, which is 8 in this case. Therefore, the output is 8.
Here are some key differences between bitwise and logical operators:
| Bitwise Operator | Logical Operator | |
|---|---|---|
| Usage | Binary operation | Logical operation |
| Target | integer value | Boolean in most case |
| Return Value | Bitwise result (integer) | One of the operands |
| Precedence | High | Low |
| Evaluation | All operands | Does not evaluate second operand if first operand is False |
| Boolean | Treats True as 1, False as 0 | Uses boolean class as is |
| in Expression | Perform AND operation bit by bit | Evaluates logical truth of entire expression |
Bitwise Operations in Python
Bitwise Operations can be easily understood by the following images:
| AND | OR |
|---|---|
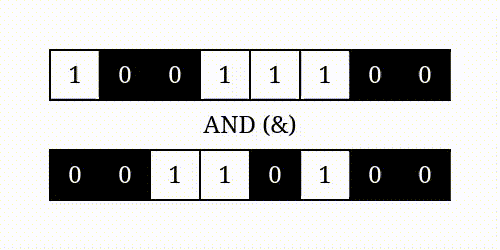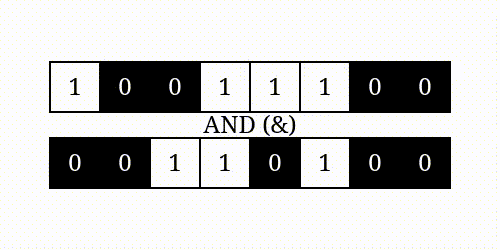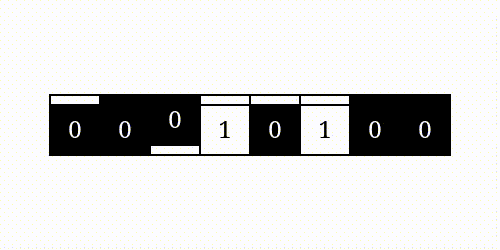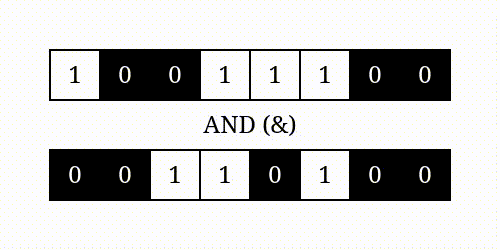 |
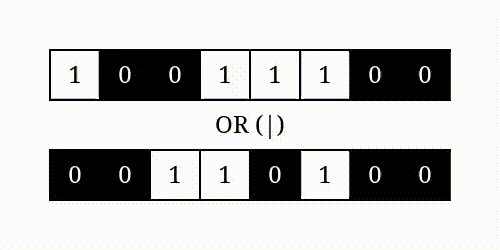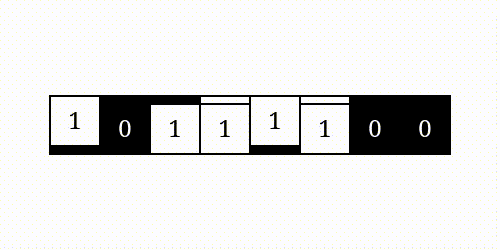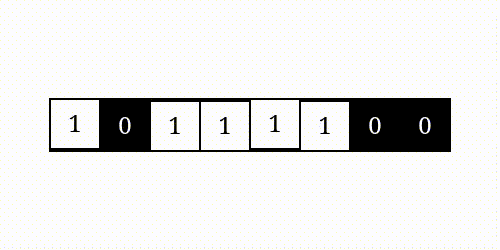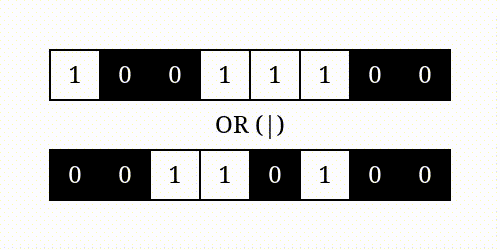 |
| XOR | NOT |
|---|---|
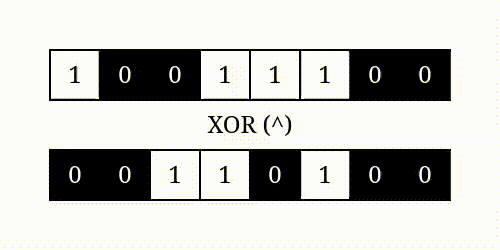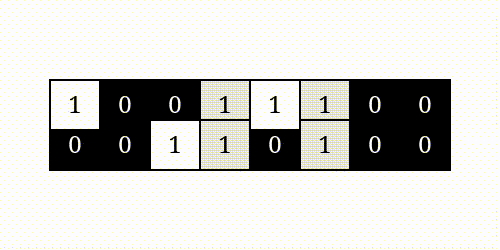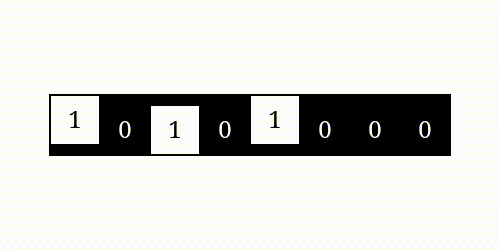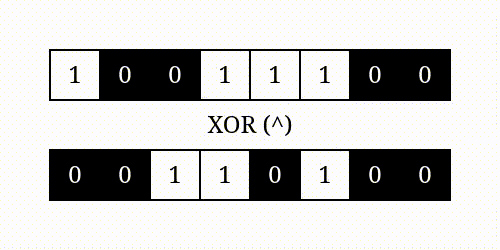 |
 |
Shift Operators
Operators above are compare the bits of two numbers. However, << and >> operators works tricky. << and >> operators called left shift and right shift operators. They shift the bits of a number to the left or right.
In terms of shift operators, it is important to note what shifting means in binary numbers. Shifting to the left means multiplying the number by 2, likewise shifting to the right means dividing the number by 2. Remind that every digit in binary number is power of 2.
Left shift operator shifts the bits to the left, and fills the empty bits with 0. Let’s see how it works in Python.
# Bitwise Left Shift
number = 5
print(f"The binary of {number} is {bin(number)}")The binary of 5 is 0b101Decimal number 5 is represented in binary as 101(2). When shifted to the left by 1, the result is 1010(1), which is same as \(5 * 2^{1}\).
shifted = number << 1
print(f"Left Shifted by 1: {shifted} ({bin(shifted)})")
print(f"Left shifted by 1 is equal to {number} * 2 = {number * 2}")Left Shifted by 1: 10 (0b1010)
Left shifted by 1 is equal to 5 * 2 = 10Likewise, when shifted to the left by 2, the result is 10100(4), which is same as \(5 * 2^{2}\).
shifted_2 = number << 2
print(f"Left Shifted by 2: {shifted_2} ({bin(shifted_2)})")
print(f"Left shifted by 2 is equal to {number} * 4 = {number * 4}")Left Shifted by 2: 20 (0b10100)
Left shifted by 2 is equal to 5 * 4 = 20How about shifting to the left by 7? The result is 1010000000(128), which is same as \(5 * 2^{7}\). Only adding 7 zeros to the right is the same as multiplying by 128.
shifted_7 = number << 7
print(f"Left Shifted by 7: {shifted_7} ({bin(shifted_7)})")Left Shifted by 7: 640 (0b1010000000)There is right shift operator either. Right shift operator shifts the bit to the right, which is equivalent to dividing the number by 2. Let’s bring back shifted_7 to the original number.
print(f"The Original number is {number} ({bin(number)})")
print(f"Left Shifted by 7 was {shifted_7} ({bin(shifted_7)})")The Original number is 5 (0b101)
Left Shifted by 7 was 640 (0b1010000000)# Bitwise Right Shift
shifted_back = shifted_7 >> 1
print(f"Right Shifted by 1: {shifted_back} ({bin(shifted_back)})")Right Shifted by 1: 320 (0b101000000)shifted_back_2 = shifted_7 >> 2
print(f"Right Shifted by 2: {shifted_back_2} ({bin(shifted_back_2)})")Right Shifted by 2: 160 (0b10100000)# ...
shifted_back_7 = shifted_7 >> 7
print(f"Right Shifted by 7: {shifted_back_7} ({bin(shifted_back_7)})")Right Shifted by 7: 5 (0b101)\[a << n = a \times 2^{n}\] \[a >> n = a \div 2^{n}\]
Bitwise shift operators are useful in optimization. Computers can not multiply or divide numbers directly. They can only add and subtract. Therefore, multiplying or dividing large numbers takes a large amout of computation. However, shifting bits is much faster than multiplying or dividing. This is why shift operators are used in low-level programming.
This is theoretical explanation, but in real-world, compilers and interpreters are smart enough to optimize the code. Python is a high-level language, which means readability is more important than slight performance improvement. Therefore, using shift operators as a means of premature optimization is not recommended.
Normally, dividing operation works same in positive and negative numbers. However, right shift operator works differently in negative numbers because of the way negative numbers are represented in binary.
Computer uses two’s complement1 to represent negative numbers. In two’s complement, the most significant bit (MSB) is used as a sign bit. If the sign bit is 1, the number is negative. When right shifting a negative number, the sign bit is copied to the empty bits. This is called sign extension2.
# Right Shift Operator with negative number
def show_bits(num, bits=8):
"""
Show the integer number in binary format
"""
if num < 0:
# Represent negative number as a two's complement
num = (1 << bits) + num
return format(num, f'0{bits}b')The function above is implementation of showing the binary bits of a number. If the number is negative, it convert the number to two’s complement. First, extend the bits to determined length of bits, which is 8 in this case. Then, add the number to \(2^{bits=8}\). As added number is negative, it is same as subtracting the number from \(2^{bits=8}\). This is how two’s complement works, that is flipping the bit values.
Now, every number will be shown in positive number with 8 bits. In this callout, there are 2 examples of right shift operator with negative numbers.
- The result of right shift is rounded down to the negative direction.
# Right shift of negative number
print(f"Right Shift of -5: {show_bits(-5)} >> 1 = {show_bits(-5 >> 1)}")
print(f"Right Shift of -6: {show_bits(-6)} >> 1 = {show_bits(-6 >> 1)}")Right Shift of -5: 11111011 >> 1 = 11111101
Right Shift of -6: 11111010 >> 1 = 11111101The right shift of -5 and -6 by 1 is both -3. In fact, -5 divided by 2 should be -2.5. However, computers can only represent integers. This is why -5 >> 1 is -3.
- The sign bit is copied to the empty bits.
# Right shift of -1
print(f"Right Shift of -1: {show_bits(-1)} >> 1 = {show_bits(-1 >> 1)}")Right Shift of -1: 11111111 >> 1 = 11111111After shifting the negative number to the right, left side is filled with 1. This is because the sign bit is copied to the empty bits. Likewise, the right shift of -1 remains -1 because every bit is filled with 1.